Definition
A vector is graphically represented as a section with an arrow on its end. It constitutes a set of ordered points and consists of:
1) direction – a straight line of the vector
2) sense – expressed by the arrow of the vector
3) magnitude – described by the length of the vector in a given scale
In equations vectors are denoted in boldface (F, v, a) or an arrow above the letter symbol (
,
,
The numerical value of a vector is expressed by the means of modulus:
|
| = 5
or plain font:
F = 5
1) direction – a straight line of the vector
2) sense – expressed by the arrow of the vector
3) magnitude – described by the length of the vector in a given scale
In equations vectors are denoted in boldface (F, v, a) or an arrow above the letter symbol (
The numerical value of a vector is expressed by the means of modulus:
or plain font:
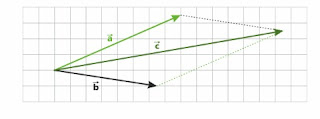
Addition of vectors
Vector addition can be done in two ways:
1) The tails of the vectors are brought to a common point and added accordingly to the parallelogram law:
=
+
2) The vectors have to be placed in such a manner that the tail of the second one (
=
+
1) The tails of the vectors are brought to a common point and added accordingly to the parallelogram law:
2) The vectors have to be placed in such a manner that the tail of the second one (
Subtraction of vectors
Vector subtraction can be done in two ways:
1) The opposite of the second vector (
=
−
=
+ ( −
)
2) Both vectors’ tails start at the same point, next their arrows are connected. The sense of the outcome vector (
=
−
1) The opposite of the second vector (
2) Both vectors’ tails start at the same point, next their arrows are connected. The sense of the outcome vector (
Scalar multiplication
The scalar multiplication does not change the direction of the vector, however, it changes its magnitude and may change its sense (when the scalar is negative). When vector A is multiplied by scalar α
B = α A
The components of vector B are of the following values:
B x = α A x ; B y = α A y ; B z = α A z
The components of vector B are of the following values:
Scalar product
Scalar product of two vectors is marked with a dot and its value is expressed by a dependency:
A • B = B • A = A B c o s α = B A c o s α
where:
A = √ A x 2 + A y 2 + A z 2
B = √ B x 2 + B y 2 + B z 2
Describes the way how two vectors see each other.B c o s α A c o s α
where:
Describes the way how two vectors see each other.
Vector product
The outcome of vector product is a new vector whose magnitude (length) is equal to the product of the magnitudes of two vectors (A, B) and the sine angle between them, the direction of the new vector C is perpendicular to the plane established by the two vectors, and its sense is established by the right hand rule or the corkscrew rule.
The order of operations here is important because A× ×
C = A× A B s i n α
The components of vector C, being a result of vector product of vectors A and B, are comprised in its magnitude and direction. However, being given the components of vectors A and B, we can calculate the components of vector C as a determinant:
C = A× |
|
where:
e x , e y , e z
The order of operations here is important because A
C = A
The components of vector C, being a result of vector product of vectors A and B, are comprised in its magnitude and direction. However, being given the components of vectors A and B, we can calculate the components of vector C as a determinant:












0 Comments
Please share your opinions and suggestions with us.